4.1 Summary and Reporting
4.2 Q7: Time Analysis by LSTM
Can time series modeling reveal a predictive link between the sentiment and buy signals in Reddit discussions about Dogecoin and its price trends, enabling us to forecast future movements based on online discourse?
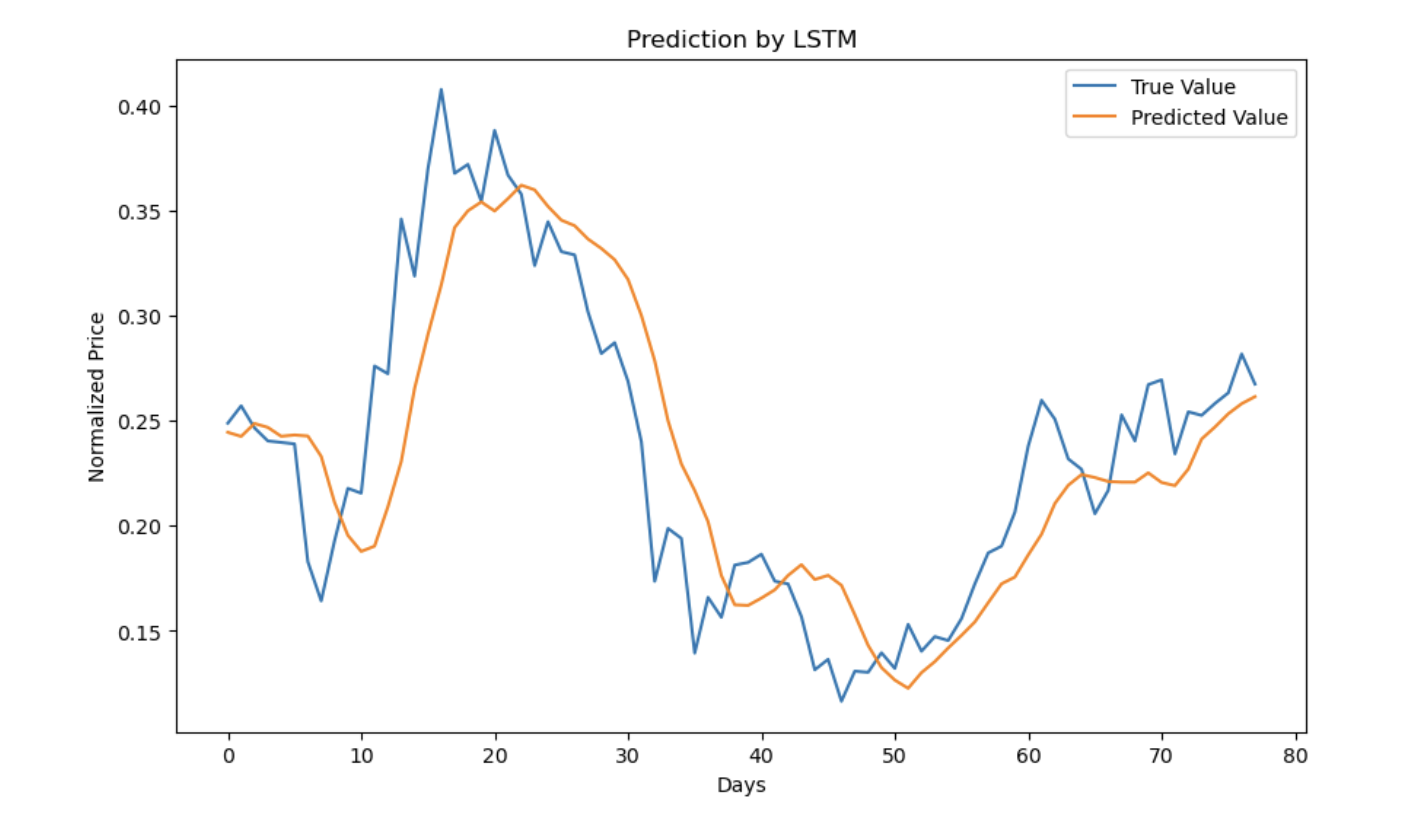
We attempt to predict the price of dogecoin using LSTM (Long Short-Term Memory). LSTM is a type of Recurrent Neural Network that is well-suited for time-series analysis and capable of understanding temporal relations in the data. We use a window of data to predict future data. In our attempt, we extracted the positive, negative, and neutral sentiment scores from a sample of the data and used them as features for the model. Consequently, the closing price, positive, negative, and neutral sentiment scores along with the number of posts and comments were used to predict the closing price of Dogecoin. Using a window of 7 days of data to predict, we make predictions and compare them to the original value. From the plot of predictions versus the original values, we can see that the model is capable of making close predictions with some lag to the trajectory traced by the original values. The model has an R^2 of 71.2%. This was higher than other window sizes of 10, and 21.
4.3 Q8: Exploring the Time Analysis by ARIMA
Building on the univariate analysis provided by LSTM in the previous section, this segment introduces VAR and ARIMA models to explore multivariate effects. These methods allow us to consider the impact of Reddit post content on Dogecoin price by incorporating multiple time series variables, thus enabling a more comprehensive analysis of how social media influences cryptocurrency markets.
4.3.1 - ARIMA(p, d, q) Model Equation
The ARIMA model combines autoregressive (AR) elements, differencing for stationarity (I), and moving average (MA) components. It is denoted as ARIMA(p, d, q), where:
- $ p $: Number of autoregressive terms
- $ d $: Number of nonseasonal differences needed for stationarity
- $ q $: Number of lagged forecast errors in the prediction equation
Differencing (I)
To achieve stationarity, the series is differenced $ d $ times. The differenced series $ ^d y_t $ is calculated as:
\[ \nabla y_t = y_t - y_{t-1} \]
Autoregressive (AR) Part
The AR part involves using $ p $ past values:
\[ \phi_1 y_{t-1} + \phi_2 y_{t-2} + \dots + \phi_p y_{t-p} \]
where $ _1, _2, , _p $ are coefficients of the model.
Moving Average (MA) Part
The MA part incorporates the errors from $ q $ past forecasts:
\[ \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \dots + \theta_q \epsilon_{t-q} \]
where $ *{t-1},* , $ are the error terms from previous forecasts, and $ _1, _2, , _q $ are coefficients.
Combined ARIMA Equation
Combining these components, we run two ARIMA models with price and buy signals as dependent variables:
Model for price (\(p=1\), \(d=1\), \(q=1\) ) \[ price_t' = c + \phi_1 price_{t-1}' + \theta_1 \epsilon_{t-1} + \epsilon_t \]
Model for buy signals (\(p=1\), \(d=0\), \(q=1\) )
buy_signals is already stationary, so we don’t need to difference it again.
\[ buy\_signals_t = c + \phi_1 buy\_signals_{t-1} + \theta_1 \epsilon_{t-1} + \epsilon_t \]
where: - $ y_t’ $ is the differenced series (if $ d > 0 $) or the original series (if $ d = 0 $) - $ c $ is a constant (intercept) - $ _t $ is the error term of the current time point.
Core Results of ARIMA Models
Table Summary
| Result | Dep. Variable | Observations | AIC | BIC | Log Likelihood | Const/Coef | AR.L1 | MA.L1 | Sigma^2 |
|---|---|---|---|---|---|---|---|---|---|
| Res 1 | n_buy_sig |
6586 | 45463.716 | 45490.887 | -22727.858 | 11.5079 | 0.8265 | -0.1053 | 58.2006 |
| Res 2 | price |
6586 | -67490.359 | -67469.981 | 33748.179 | NA | -0.4687 | 0.4380 | 2.07e-06 |
Interpretation of Results
Res 1 (n_buy_sig): The ARIMA(1, 0, 1) model for
n_buy_sigdemonstrates good predictability with a significant AR1 coefficient of 0.8265, suggesting a strong autoregressive term. The negative MA1 coefficient (-0.1053) indicates a slight adjustment in the opposite direction of the error term from the previous period. The model has a relatively high AIC and BIC, pointing to the complexity of the model but a necessary fit for the data characteristics.Res 2 (price): For the
pricevariable modeled with ARIMA(1, 1, 1), the coefficients for both AR1 and MA1 are significant but with opposite signs, suggesting partial offsetting effects. The model achieves an extremely low AIC and BIC, indicating an excellent fit. The Log Likelihood is exceptionally high, which, combined with a very low sigma^2, points to a highly effective model for forecastingprice.
4.3.2: Vector Autoregression (VAR)
Vector Autoregression (VAR) is a statistical model used to capture the linear interdependencies among multiple time series. VAR models generalize the ARIMA model by allowing more than one evolving variable. Each variable in a VAR model is a linear function of past lags of itself and past lags of the other variables. This makes VAR suitable for systems where the variables influence each other.
A VAR model describes each variable with an equation that combines:
- The variable’s own lags (autoregressive part).
- The lags of other variables in the system.
To illustrate the standard form of a VAR model for variables $ y_t $ and $ x_t $, the equations for this system can be expressed as:
\[ \begin{align*} y_t &= c_1 + \phi_{11} y_{t-1} + \phi_{12} x_{t-1} + \epsilon_{1t} \\ x_t &= c_2 + \phi_{21} y_{t-1} + \phi_{22} x_{t-1} + \epsilon_{2t} \end{align*} \]
Where: - $ c_1 $ and $ c_2 $ are constants (intercepts of the equations). - $ *{11} $, $* $, $ *{21} $, and $* $ are the coefficients of the lagged values of $ y $ and $ x $. - $ *{1t} $ and $* $ are the error terms, assumed to be white noise.
Condensed Summary of VAR Model Results
| Equation | Lag | Coefficient | Std. Error | t-stat | Prob |
|---|---|---|---|---|---|
| price_s | |||||
| L1.price_s | -0.027636 | 0.012353 | -2.237 | 0.025 | |
| L2.price_s | 0.031450 | 0.012355 | 2.546 | 0.011 | |
| L7.price_s | 0.041803 | 0.012343 | 3.387 | 0.001 | |
| L9.price_s | 0.033151 | 0.012362 | 2.682 | 0.007 | |
| L11.price_s | -0.025686 | 0.012359 | -2.078 | 0.038 | |
| n_buy_sig | |||||
| L1.n_buy_sig | 0.707021 | 0.012347 | 57.265 | 0.000 | |
| L2.price_s | -136.544667 | 64.626404 | -2.113 | 0.035 | |
| L4.n_buy_sig | 0.068851 | 0.015113 | 4.556 | 0.000 | |
| L7.price_s | 178.560081 | 64.568315 | 2.765 | 0.006 | |
| L10.n_buy_sig | 0.034079 | 0.015100 | 2.257 | 0.024 | |
| L11.n_buy_sig | 0.036609 | 0.012330 | 2.969 | 0.003 |
Equation for price_s
\[ price_{s,t} = -0.027636 \cdot price_{s,t-1} + 0.031450 \cdot price_{s,t-2} + 0.041803 \cdot price_{s,t-7} + 0.033151 \cdot price_{s,t-9} - 0.025686 \cdot price_{s,t-11} + \epsilon_{t} \]
Equation for n_buy_sig
\[ n\_buy\_sig_t = 0.707021 \cdot n\_buy\_sig_{t-1} - 136.544667 \cdot price_{s,t-2} + 0.068851 \cdot n\_buy\_sig_{t-4} + 178.560081 \cdot price_{s,t-7} + 0.034079 \cdot n\_buy\_sig_{t-10} + 0.036609 \cdot n\_buy\_sig_{t-11} + \epsilon_{t} \]
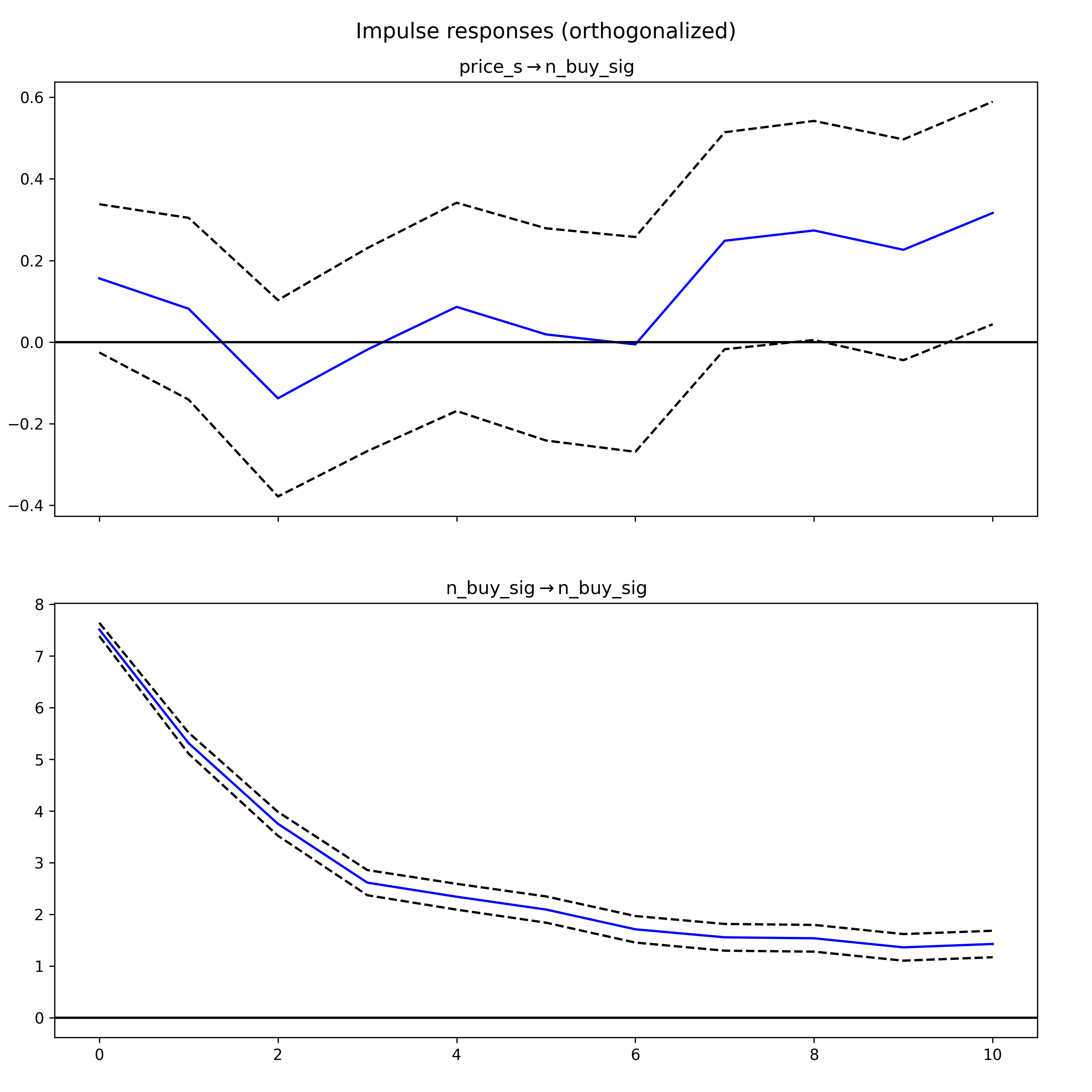
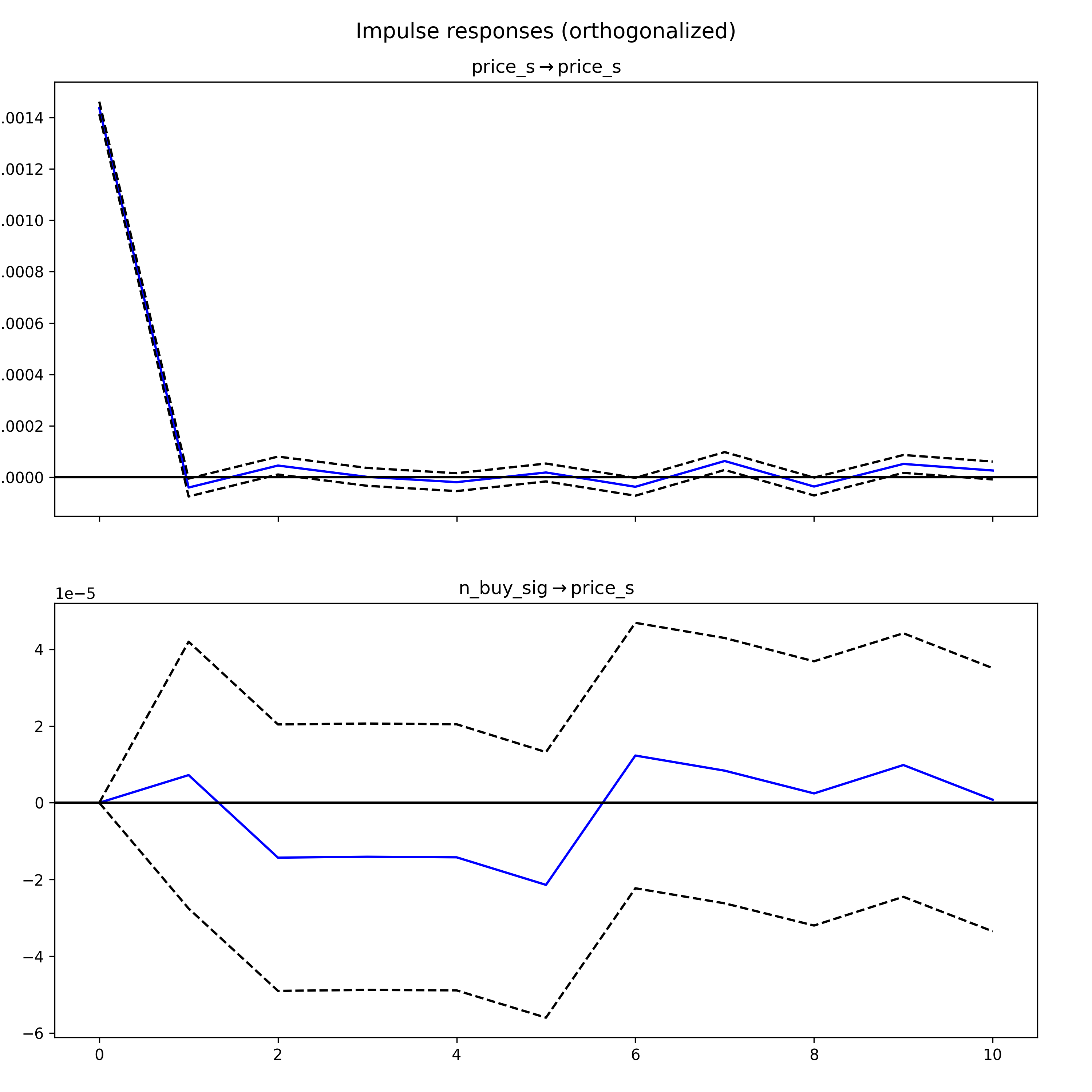
Impulse response functions (IRF)
In Vector Autoregression (VAR) models, an IRF maps the reaction of endogenous variables in the model to a one-unit increase in the shock variable, holding all else constant. In the following IRF chart, the response of price_s (differenced price for stationarity) to a shock in n_buy_sig is displayed over several hours.
The components of an IRF plot are explained below:
- X Axis: Displays the time intervals following a shock (hours)
- Y Axis: Measures the magnitude of the response from the dependent variable ($ for price, number of buy signals)
- Blue Line: Represents the estimated response of the variable to the shock across different time periods.
- Dashed Lines: These indicate the confidence intervals, showing the range where the true response likely falls, typically with a 95% confidence level.
A response line that crosses the zero line signifies changes in the direction of the response over time.
(If the confidence interval includes the zero line, it indicates that the response is not statistically significant at those points.)
In the first IRF graph, the response of “price_s” to shocks in “n_buy_sig” is observed. Initially, the response drops below zero, indicating a negative impact, before oscillating around zero. This pattern suggests an immediate negative reaction followed by ongoing uncertainty in both the direction and magnitude of the impact.
The second IRF graph examines the response of “n_buy_sig” to shocks in “price_s.” The response begins at zero, then dips into the negative territory and exhibits a pattern of oscillation that gradually returns toward zero. The diminishing amplitude of the response over time suggests that the impact of the shock lessens as time progresses.
4.4 Q9: Exploring the casual relationship between Big Events and Community Behavior
[🔗Github Link]
4.4.1 How Big Events impact price?
In Question 6, from figure 4, we find that after the Elon Musk tweeted a picture of Shiba wearing a Twitter T-shirt. The price of dogecoin suddenly get a upheavel. We assume that would also apply on the discussion volume and behavior of dogecoin community in reddit. In this part, we would use machine learning based casual inference method to find if there is a casual relationship between Big Events such as Elon Musk’s tweets and the behavior of reddite dogecoin discussion.
Two indicators would be tracked as a representation of overall discussion behavior, sentiment and buy signal mentioned. Both of them are highly related to the price change. In such dynamics, the behavior change caused by Big Events are revealed in the markert.
Synapse ML
For our casual inference, we are using Synpase ML package to conduct casual effect analysis and heterogeneous effect. SynapseML (previously known as MMLSpark), is an open-source library that simplifies the creation of massively scalable machine learning (ML) pipelines which provides simple, composable, and distributed APIs for a wide variety of different machine learning tasks.
4.4.2 Causal Inference
We select the 14 days a window of 14 days before and after November 1, 2022, when the tweet of Elon Musk was made.
Treatment: Before or After Tweet Post Outcome: Average Sentiment/ Buy Signal Proportion
| Treatment Effect | Confidence Interval | If Casual | |
|---|---|---|---|
| Sentiment | 0.06 | (0.0376, 0.0824) | Yes |
| Buy Signal | 0.324 | (0.1141, 0.4499) | Yes |
The table shows the treatment effect size for sentiment is relatively modest (0.06). This suggests that while Elon Musk’s tweet had a positive impact on the sentiment of Dogecoin discussions, the change is not overwhelmingly large but is statistically significant. This subtlety in sentiment change might imply that while influential tweets can sway public opinion, they do not necessarily transform overall sentiment drastically unless accompanied by significant market events.
The treatment effect for buy signals is notably larger (0.324), indicating a more pronounced behavioral response in terms of purchasing or trading interest. This larger effect size underscores the potential of prominent figures in social media to trigger actionable responses, possibly due to the perceived endorsement or speculative optimism driven by the tweet.
We find that there is a statistical casual relation between Elon Musk’s tweet and the sentiment and buy signal proportion of Dogecoin discussions on Reddit. The tweet has a positive impact on both sentiment and buy signals, which ultimately impact the market and create a upheavl in price.
4.5 Q10: Exploring the Network Structure
We seek to elucidate the network structure within the realms of the r/dogecoin and r/cryptocurrency subreddits to discern community clustering patterns and the dissemination dynamics of information therein. Our methodology entails an initial identification of unique posts within these Reddit communities, followed by the construction of edges between posters and commenters. These edges are endowed with weights; specifically, a weight of 1 is assigned when a commenter engages with a post authored by a unique poster, and a weight of ‘n’ is assigned if multiple comments emanate from a single commenter directed towards the same author. It is pertinent to note within this network configuration that a comment can engender multiple posts, while conversely, a single post may attract contributions from multiple commenters. Following the reformatting of the dataset in accordance with the aforementioned relationships, we export the resultant network to a GML file format, wherein each node represents a distinct user participating in the network either as a poster or a commenter.

Subsequently, the network undergoes visualization using Gephi, yielding insights into its structural characteristics. The visualization reveals a decentralized topology, wherein numerous peripheral communities are observed to coalesce, yet no singular ‘central user’ or pivotal opinion leader emerges prominently. From a statistical standpoint, the network comprises 73,395 nodes and 209,864 edges, suggesting a propensity for sparse connectivity. The average degree, indicative of the average number of connections per node, stands at approximately 2.859, further underscoring the network’s distributed nature. Modularity analysis yields a value of 0.383, denoting the extent of decentralization into distinct communities within the network. Specifically, partitioning reveals the existence of 14 discernible communities or groups, delineated by inter-nodal connections. The average clustering coefficient, a measure of local interconnectedness, is computed at 0.022, suggesting modest clustering tendencies within the network. Finally, the average path length, reflective of the average number of steps required to traverse between any two nodes, is determined to be 4.225, providing insights into the network’s navigational efficiency.
In summation, our analysis furnishes a comprehensive overview of the network’s structural attributes, elucidating its decentralized architecture and community clustering dynamics. Through meticulous statistical scrutiny, we delineate key metrics encapsulating connectivity, modularity, clustering, and navigational efficiency, thereby enriching our understanding of information propagation within these Reddit communities.
